Code as a Liberal Art, Spring 2021
Unit 1, Exercise 2 lesson — Wednesday, January 26
Coding algorithms
Today we're going to go from the abstract idea of what algorithms are to actually implementing some algorithms in computer program code. We're going from the first exercise where you devised an algorithm for sorting a deck of cards, to implementing some algorithms in Python to sort numbers, words, and even filtering the pixels of an image.
So often in discussions of digital media, we talk about and theorize algorithms in general terms, as abstract, formal sequences of instructions. So much recent socio-political study of technology has rightly realized the need to reckon with the power and prevalence of algorithms and the ways they shape daily life, from shopping to socializing to how we acquire news. And while introductory computer programming and creative coding education typically claims to educate about how algorithms actually work, the fact is that most of the coding that we do in those contexts does not actually involve puzzling through the implementation of algorithms of the kinds studied by computer scientists, nor of the kinds that have become such influential mediators of our socio-cultural patterns. Today we're going to work through some exercises that might hopefully help you start to fill in that gap.
 (An IBM 082 punch card sorting machine. You can
find more
information about this here.)
(An IBM 082 punch card sorting machine. You can
find more
information about this here.)
But first we're going to have to talk about some preliminaries to get setup to do that work ...
The command line
- We'll be using several tools and platforms throughout the semester. We're going to start off working with Python on the command line.
-
The command line is a type of user interface. Usually when we think about user interfaces we think about interactive motion graphics, which we usually call GUIs for graphical user interfaces. The command line is a user interface too, but it is an interface primarily operated through text.
There are many reasons why we are saddled with this text-based mode and metaphor for interacting with computer programs. If you would like to learn about some history of the command line and how it came to be, you can watch this video where I walk through part of that story (25 min). I made this for my "Radical Software" class last semester, so please ignore that on the title slide. I also refer to a twitter project, which we won't be doing in this class.
Suffice it to say, the command line (sometimes called the terminal, or a shell) is a computer program in which you type the names of other programs (called commands) which the shell then executes. These commands can be common operating system utilities, like listing the contents of a folder, and they can also be computer programs that you write, which is what we'll get started with today.
As I explain in the above video, a big part of the persistent usefullness of the command line today is that it is often much easier to write computer programs with text-based user interfaces than with more user friendly GUIs. Often times a GUI will require dozens of extra lines just to get started, whereas a command line program can get right to algorithms or data processing without the extra code to make it more visually appealing or user friendly.
-
Find the command line on your computer. On a Mac, the easiest way to access the command line is with a program called Terminal. Open up Finder, go into the "Applications" folder, look for a folder called "Utilities", and within that, find and double-click on "Terminal". Or you can use a Spotlight search (⌘-SPACE) and search for "Terminal". When you open that, it should look like this:
but with different colors. You can customize your colors in Preferences.
On Windows, please reach out to me and we can work together to get you setup.
-
Throughout the semester, whenever I am including command line instructions, I will display them in a white, fixed-width font on a black background with rounded gray corners like this:
$ echo "Hello, world" Hello, world
Or for shorter commands, I'll use a single line of white, fixed-width text on a black background:like this.(I try to make this formatting easily visible for everyone, even those who might have different seeing abilities. If I can help make this more legible for you, please let me know!)
I (and many others) use the dollar sign
$to indicate the prompt where you can type, and the text that comes after is valid syntax that you can copy/paste into your command line. Your prompt may look different — that is also a customizable setting. And you don't type the dollar sign. The lines that come after (the lines not beginning with a dollar sign) are meant to indicate what the command line will display back to you. You can go ahead and try typing the command above. You should get the same result as me. -
We won't be using too many command line instructions. I will explain them as we need them. For now, here are a few useful ones:
-
pwd: print working directory, displays the name of the current directory that you are in. In the command line context, folders are called directories. -
cd: change directory, changes the directory (folder) that you are currently in. -
ls: list, lists the contents of the current directory. That is a lower-case "L", not the number "1".
If a command is running and you want to stop it, you can type CONTROL-C. If you want to exit your shell program, you can type
exitor press CONTROL-D, then you can close the window. -
-
Let's get started by creating a new folder in Finder for this exercise. I recommend that you create a folder for this class where you'll put everything this semester, within that create a folder just for project work, and within that create new folders for each lesson. So your folder structure should look like this so far:
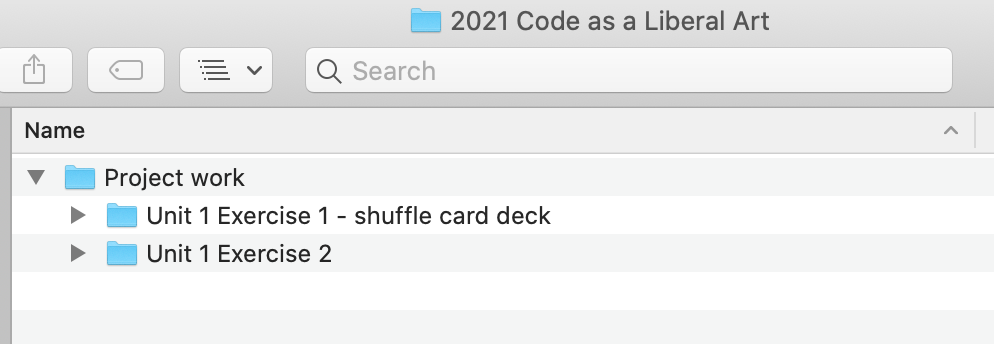
On Mac, there is some nice and convenient interaction between the Finder GUI and the command line. So in your Terminal window, type
cd, and then actually drag the "Unit 1 exercise 2" folder into the Terminal and press enter. If you wish to typepwd, that should confirm that you are now in this folder/directory.
Python
Next let's introduce Python in the command line context.
-
From the command line, you should simply be able to type
pythonto invoke the Python shell:$ python Python 3.8.3 (v3.8.3:6f8c8320e9, May 13 2020, 16:29:34) [Clang 6.0 (clang-600.0.57)] on darwin Type "help", "copyright", "credits" or "license" for more information. >>>
You may not see precisely the same output, but it should be similar. If you seePython 2.7.xlet me know.Noteworthy here is that the prompt has changed to
>>>. This is to indicate that you are not in the operating system shell, but rather in the Python shell. At this point, you can no longer type the regular shell commands (likecdandpwd) and instead can type any valid Python syntax. Try some:>>> a = 5 >>> print(a) 5 >>> print(a+5) 10
To exit the Python shell back to the command line, you can type CONTROL-D orexit().
Atom
You can do a lot with just the Python shell. But if you want to write executable computer programs, you need to type them up into a text file. For this, we'll be using Atom.
-
Open up Atom. Start by closing all the tabs and help screens. Then, drag your "Unit 1 exercise 2" folder into the Atom window. You should now see something like this:
-
Click File > New File. Now you can type Python syntax into this file and save it. Try this:
a = 5 print(a) print(a+5)
Throughout the semetser, I will indicate valid Python code in a file with this fixed-width font on a light blue background. Whenever you see this, it should be valid Python code that you can copy/paste into your file. Again, if I can help make this more legible to you, please let me know! -
Now, save this file by click File > Save, or pressing ⌘-S on Mac. Name your file
start.py.Now, you should be able to flip back over to Terminal, and run this simple Python program. Remember to first exit out of the Python shell by typing CONTROL-D. If you'd like, first make sure that you are in the right directory:
$ pwd /Users/rory/Documents/.../Code as a Liberal Art/Project work/Unit 1 exercise 2 $ python start.py 5 10
Your directory path may not be the same as mine (hence my "...") but otherwise you should see the same output.
Great! Now we can get started coding in Python.
Coding algorithms
Let's pause here and think about how you would design the following algorithm:
Find the smallest number in a list of numbers.(Similar to command line code and Python code, I will use this gray background with thin double-borders to indicate "pseudocode": this is not valid programming language syntax, but is plain English that is meant to read algorithmically. It is a kind of in-between step in the process of translating from human communication to machine instructions.)
It might be hard to actually think through the process that your brain is going through when you find the smallest number in a list. Maybe it will help if we consider an actual list of (basically random) numbers:
 (I have referred to the first one starting with zero because
that is what nearly all computer programming languages do.)
(I have referred to the first one starting with zero because
that is what nearly all computer programming languages do.)
If you are like me, your mind may have done something like this:
Look at the first number, and let's call that "the smallest number" for the moment. Now, compare the next number to "the smallest number": if the next number is smaller than "the smallest number", then it now becomes the smallest. Repeat this for every other number. At the end of the list, "the smallest number" will be smaller than all the others.
Let's try to translate this into Python code. Create a new file in Atom (File > New File) and type this there.
Start by entering the list of numbers. Here is the Python syntax for that:
number_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ]Now, let's implement the first part of the algorithm:
number_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ]
smallest_number = number_list[0]
(When working through coding examples, I will indicate newly
added code in blue with a dotted underline.)
This new syntax says take the first item in the list
(the [0]) and assign that to a variable
called smallest_number.
The next part of the algorithm indicated
repetition: Repeat this for every other
number. In Python, we do that with a for
loop, and the syntax looks like this:
number_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ] smallest_number = number_list[0] for n in number_list: if n < smallest_number: smallest_number = nThat will loop over every number in the list, and temporarily refer to each one as
n. Each time the loop executes, it will
compare n (the current number in the list) to
the current smallest number
(i.e. smallest_number) and if n is
smaller, it now becomes the smallest number.
That's it! That's all there is to this algorithm. Now we can just print an informative message at the end:
Example 1: Find the smallest number
number_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ]
smallest_number = number_list[0]
for n in number_list:
if n < smallest_number:
smallest_number = n
print("The smallest number in this list is: " + str(smallest_number) )
The str() command converts the number into text
(called a string). And the plus sign in this
case (+) is not addition, but string
concatenation: it just appends one string onto another.
Save this file in Atom (File > Save) and name
it unit1-smallest_number.py.
Try running this file from the command line and see what happens:
$ python unit1-smallest_number.py The smallest number in this list is: 1Perhaps not the most exciting output, but part of what is great here is that you could modify this list, even adding thousands of numbers, and the algorithm would still work well.
Swapping out text for numbers
One great thing about Python is that many of
the comparison operators
(e.g. < and >) work equally well
for text as for numbers. This will be an exercise in the
homework.
Sorting
Let's try a slightly more complicated algorithm: putting a list of numbers in order. Computer scientists call this sorting - perhaps somewhat of a misnomer.
Thinking back to your card sorting algorithm, how might we describe a strategy to put a list of numbers into increasing order?
Using some of the same principles from our Smallest Number algorithm, let's try this:
Given a list of unordered numbers
Make a new, empty list
Put the first item from the unordered list into the new list
Now consider the next item in the unordered list:
If it is smaller than the item in the new list, then put it first
If it is larger than the item in the new list, put after
For each subsequent item in the unordered list, find where it fits into the new list.
In other words:
For each item in the unordered list:
Compare it to each item in the new list:
If it is bigger, move on
If it is smaller, insert it before
Let's implement this in Python as well. Make a new file in Atom (File > New File). Start with the input list again:
unordered_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ]
Now we'll make a new, empty list, like this:
unordered_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ]
new_list = []
Now, as I described, take the first item from the unordered list and put it into the new list:
unordered_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ]
new_list = []
new_list.append( unordered_list[0] )
unordered_list[0] is how we reference the first
item in the unordered list, and .append() is the
command to add an item to a list.
Next we'll add a loop, to loop over all the items in the unordered list:
unordered_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ] new_list = [] new_list.append( unordered_list[0] ) for item in unordered_list: # something will go in here ...By the way, any line that starts with
# is a
comment and Python ignores it.
What do we do with each item from the underline
list? We have to check it against each item in the new list. So
we need another loop. This one will look a little different:
unordered_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ]
new_list = []
new_list.append( unordered_list[0] )
for item in unordered_list:
j = 0
while item > new_list[j]:
j = j + 1
new_list.insert( j, item )
This is a new control structure called
a while loop. This new variable j
starts out as 0. Then we compare the item from the
unordered list with the first item of the new list. If it is
greater, we increase j and keep repeating this
process. But as soon as the item is not greater than
the next item in the new list, we'll have found the place where
it belongs. In other words, j will indicate its
position. So we can use the .insert() command to
insert item at the position indicated
by j.
There's only one last problem. Try saving this and running it. You will probably get an error message like this:
$ python unit1-insertion-sort.py
Traceback (most recent call last):
File "unit1-insertion-sort.py", line 14, in <module>
while item > new_list[j]:
IndexError: list index out of range
The problem here occurs when item is greater than
everything in the new list. So this while loop gets
to the very end, and j is bigger than the size of
the list. So the insert gives an error. We can fix it with the
following check:
unordered_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ]
new_list = []
new_list.append( unordered_list[0] )
for item in unordered_list:
j = 0
while j < len(new_list) and item > new_list[j]:
j = j + 1
new_list.insert( j, item )
This will guarantee that j does not get too
big.
Save this, run it again, and you shouldn't any error
messages. But did it work? Add some print()
statements to watch the new list getting sorted as the algorithm
runs.
Example 2: Insertion sort
unordered_list = [ 234, 2, 6, 42, 1, 124, 687, 5, 674, 45, 67, 99, 23 ]
new_list = []
new_list.append( unordered_list[0] )
print(new_list)
for item in unordered_list:
print(item)
j = 0
while j < len(new_list) and item > new_list[j]:
j = j + 1
new_list.insert( j, item )
print(new_list)
Images
I've talked about how this first unit of the course will be focused on digital formalism and examination of some of the fundamental forms of computational media: bits, pixels, images, files. Many of the principles touched on in the above coding examples can be applied to these digital forms, and we will explore these techniques in the coming weeks.
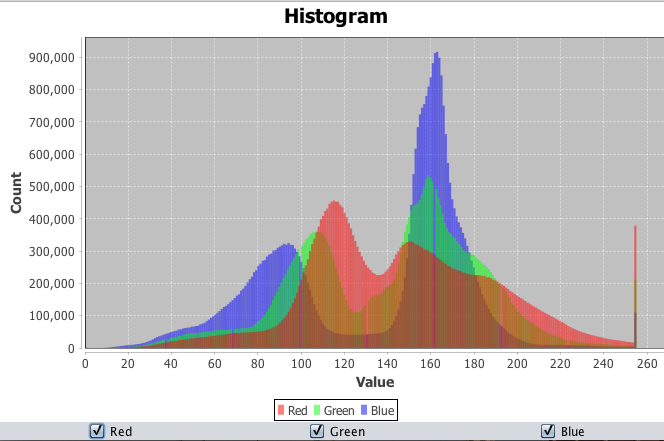

The image on the left is a histogram that shows the relative amounts of various color components (red, green, and blue) in a digital image. The image on the right is the result of a filter applied to replace all colors in the image with only 4 or 5 colors, determined based on the brightness of pixels in the original.
For example, the below code sample opens an image and applies a filtering algorithm which loops over the image, pixel by pixel, checking each one for brightness. Pixels that are below a certain level of brightness are simply replaced with white. A sample output of what this looks like is below.
Example 3: Filtering image pixels
from PIL import Image
from PIL import ImageColor
img = Image.open("fire.jpg")
new_img = img.convert(mode="HSV")
(width,height) = new_img.size
for x in range(width):
for y in range(height):
if new_img.getpixel((x,y))[2] < 50:
new_img.putpixel( (x,y), ImageColor.getcolor("white","RGBA") )
new_img.convert(mode="RGB").save("new.jpg")


Wrapping up ...
Hopefully this gives you some building blocks in algorithmic thinking that you can play with. The homework for this week has some opportunities for you to experiment with these ideas. Have fun!